
In recent years, the power efficiency of embedded multimedia applications (e.g. medical image processing, video compression) with simultaneous consideration of timing constraints has become a crucial issue. Many of these applications are data-dominated using large amounts of data memory. Typically, such applications consist of deeply nested for-loops. Using the loops' index variables, addresses are calculated for data manipulation. The main algorithm is usually located in the innermost loop. Often, such an algorithm treats particular parts of its data specifically, e.g. an image border requires other manipulations than its center. This boundary checking is implemented using if-statements in the innermost loop. This is illustrated in the following figure representing an MPEG4 full search motion estimation kernel:
for (x=0; x<36; x++) {
x1 = 4*x;
for (y=0; y<49; y++) {
y1 = 4*y;
for (k=0; k<9; k++) {
x2 = x1+k-4;
for (l=0; l<9; l++) {
y2 = y1+l-4;
for (i=0; i<4; i++) {
x3 = x1+i; x4 = x2+i;
for (j=0; j<4; j++) {
y3 = y1+j; y4 = y2+j;
if (x3<0 || 35<x3 || y3<0 || 48<y3)
then_block_1; else else_block_1;
if (x4<0 || 35<x4 || y4<0 || 48<y4)
then_block_2; else else_block_2; }}}}}}
This code fragment has several properties making it sub-optimal w.r.t. runtime and energy consumption. First, the if-statements lead to a very irregular control flow. Any jump instruction in a machine program causes a control hazard for pipelined processors. This means that the pipeline needs to be stalled for some instruction cycles, so as to prevent the execution of incorrectly prefetched instructions.
Second, the pipeline is also influenced by data references, since it can also be stalled during data memory accesses. In loop nests, the index variables are accessed very frequently resulting in pipeline stalls if they can not be kept in processor registers. Since it has been shown that 50% - 80% of the power consumption in embedded multimedia systems is caused by memory accesses, frequent transfers of index variables across memory hierarchies contribute negatively to the total energy balance.
Finally, many instructions are required to evaluate the if-statements, also leading to higher runtimes and power consumption. For the MPEG4 code above, all shown operations are in total as complex as the computations performed in the then- and else-blocks of the if-statements.
The analysis techniques of Loop Nest Splitting as source code optimization are able to detect that
Information of the first type is used to detect conditions not having any influence on the control flow of an application. This kind of redundant code (which is not typical dead code, since the results of these conditions are used within the if-statement) can be removed from the code, thus reducing code size and computational complexity of a program.
Using the second information, the entire loop nest can be rewritten so that the total number of executed if-statements is minimized:
for (x=0; x<36; x++) {
x1 = 4*x;
for (y=0; y<49; y++) {
if (x >= 10 || y >= 14) /* Splitting-if */
for (; y<49; y++) /* Second y loop */
for (k=0; k<9; k++)
for (l=0; l<9; l++)
for (i=0; i<4; i++)
for (j=0; j<4; j++) {
then_block_1;
then_block_2; }
else {
y1 = 4*y;
for (k=0; k<9; k++) {
x2 = x1+k-4;
for (l=0; l<9; l++) {
y2 = y1+l-4;
for (i=0; i<4; i++) {
x3 = x1+i; x4 = x2+i;
for (j=0; j<4; j++) {
y3 = y1+j; y4 = y2+j;
if (x3<0 || 35<x3 || y3<0 || 48<y3)
then_block_1; else else_block_1;
if (x4<0 || 35<x4 || y4<0 || 48<y4)
then_block_2; else else_block_2; }}}}}}
In order to achieve this, a new if-statement (the splitting-if) is inserted in the y loop testing the condition x>=10 || y>=14. The else-part of this new if-statement is an exact copy of the body of the original y loop. Since all if-statements are fulfilled when the splitting-if is true, the then-part consists of the body of the y loop without any if-statement and associated else-blocks. To minimize executions of the splitting-if for values of y >= 14, a second y loop is inserted in the then-part counting from the current value of y to the upper bound 48.
As can be seen from this example, loop nest splitting is able to generate linear control flow in the hot-spots of an application. Furthermore, references to memory are reduced significantly, because large amounts of branching, arithmetic and logical instructions and induction variable accesses are removed from the code. Using these factors, loop nest splitting is able to achieve considerable speed-ups combined with reductions in energy consumption.
Due to the need for very efficient machine code and the lack of optimizing compilers, assembly-level software development for embedded processors was very common in the past. However, both embedded applications and processors are getting more and more complex, and the development of highly optimizing compilers allows the replacement of assembly level programming. Modern compilers are equipped with a large amount of different optimizations, among which Common Subexpression Elimination (CSE) and Loop-invariant Code Motion (LICM) have proven to be highly beneficial.
This page presents a new source code optimization called Advanced Code Hoisting (ACM). This technique is an elaborate combination of the already known CSE and LICM optimizations with a formal mathematical criterion steering the application of the mentioned optimizations. Studying Advanced Code Hoisting is motivated by the fact that the applocation of the conventional CSE and LICM techniques might not be beneficial if the control flow is not considered. This is illustrated by means of a source code fragment extracted from the innovative GSM codebook search depicted in the following figure:
for (j=0; j<l_code; j++)
for (i=0; i<l_code; i++) {
if (i <= c1)
if (i == c1)
rdm = h2[l_code-1-i];
else rdm = rr[i*(i-1)/2];
else rdm = rr[j*(j-1)/2];
...mul(rdm, ...);
if (i <= c2)
if (i == c2)
rdm = h2[l_code-1-i];
else rdm = rr[j*(j-1)/2];
else rdm = rr[i*(i-1)/2];
...mul(rdm, ...); }
For this small example, we assume that the symbolic constants l_code, c1 and c2 are equal to 10,000, 9,000 and 1,000, respectively. The structure of the for-loops and if-statements depicted in the above figure has the effect that the expression l_code-1-i is executed 20,000 times (i*(i-1)/2: 179,990,000 times, j*(j-1)/2: 19,990,000 times).
The application of the conventional CSE and LICM optimizations has the effect that these three expressions are replaced by accesses to new local variables which are defined in the outermost possible loops. As a consequence, both l_code-1-i and i*(i-1)/2 are moved to the beginning of the i-loop, whereas j*(j-1)/2 is moved to the beginning of the j-loop. The resulting code is depicted in the following:
for (j=0; j<l_code; j++) {
int ach_1 = j*(j-1)/2;
for (i=0; i<l_code; i++) {
int ach_2 = i*(i-1)/2;
if (i <= c1)
if (i == c1)
rdm = h2[l_code-1-i];
else rdm = rr[ach_2];
else rdm = rr[ach_1];
...mul(rdm, ...);
if (i <= c2)
if (i == c2)
rdm = h2[l_code-1-i];
else rdm = rr[ach_1];
else rdm = rr[ach_2];
...mul(rdm, ...); }}
For the given values of l_code, c1 and c2, this conventional code hoisting leads to an execution frequency of 100,000,000 for l_code-1-i and i*(i-1)/2 (10,000 for j*(j-1)/2). As can be seen, the execution frequency of l_code-1-i increases by a factor of 5,000.
The reason for this increased execution frequency after its motion to the beginning of the i-loop are the two if-statements surrounding this expression. In the original GSM code, the expression is executed only for two iterations of the i-loop. After its motion out of the if-statements, it is executed for every iteration of the i-loop resulting in the observed increased execution frequency.
The key idea of Advanced Code Hoisting is the comparison of execution frequencies during the optimization. For the GSM codebook search, only the motion of expressions i*(i-1)/2 and j*(j-1)/2 leads to reduced execution frequencies. Hence, only these expressions are eliminated and hoisted. In contrast, l_code-1-i is not changed at all. The resulting source code after ACH is shown in the following:
for (j=0; j<l_code; j++) {
int ach_1 = j*(j-1)/2;
for (i=0; i<l_code; i++) {
int ach_2 = i*(i-1)/2;
if (i <= c1)
if (i == c1)
rdm = h2[l_code-1-i];
else rdm = rr[ach_2];
else rdm = rr[ach_1];
...mul(rdm, ...);
if (i <= c2)
if (i == c2)
rdm = h2[l_code-1-i];
else rdm = rr[ach_1];
else rdm = rr[ach_2];
...mul(rdm, ...); }}
The first main contribution of ACH is the novel combination of the well-known compiler optimizations CSE and LICM with a steering criterion. Second, the formulation of this criterion deciding when to apply CSE and LICM is based on control flow aspects. Formal methods modeling large classes of loop nests and if-statements and polyhedral techniques are applied for the exact computation of execution frequencies of expressions. Third, all compilers involved during benchmarking are called with their highest levels of optimization enabled. Since they all include a CSE and LICM, it is an important observation that still very large savings can be achieved using Advanced Code Hoisting. This fact underlines that novel source code optimizations relying on already existent techniques to some extent are still able to outperform existing optimizing compilers.
The goal of source-level transformations for Memory Hierarchy Exploitation is to minimize memory footprint and system bus load. The generation of ring buffer arrays during DTSE is mainly due to two reasons. First, it is attempted to make use of a predefined memory hierarchy efficiently during the data reuse step. This is done by copying frequently accessed parts of larger data into smaller arrays which can then be kept in a smaller and thus less energy consuming memory. Hereafter, in-place mapping techniques applied to these arrays (which are also called data reuse copies) focus at minimizing the required amount of memory by reducing the size of these data reuse copies.
The effect of the data reuse transformation on a medical imaging application is illustrated schematically in the following:

In its original structure, a tomography image is processed by a pipeline consisting of three sequential steps called GaussBlur, ComputeEdges and DetectRoots. Each of these steps processes an image given as input and writes a resulting image as output which is then passed to the next stage in the pipeline.
During DTSE, data reuse copies are inserted representing buffers for entire lines of an image:
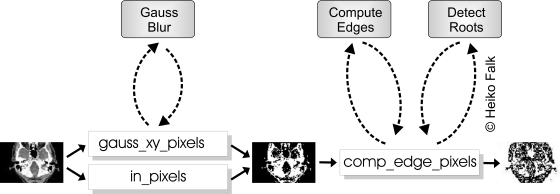
gauss_xy_pixels and comp_edge_pixels contain three individual lines of the image, namely the ones currently processed by the GaussBlur and the ComputeEdges steps respectively, together with their direct neighbors. The third line buffer in_pixels consists of only one line which is also requires during the GaussBlur computation.
These line buffers are subject to the subsequent in-place mapping stage of DTSE. Not surprisingly, the line buffers are traversed in a straight forward fashion from the left edge of the image to the right one. But at every individual position (x, y) during this traversal, only the immediate neighbors of the currently examined pixel within a line buffer are referenced:

Due to this property, only the neighboring pixels of the current (x, y)-position need to be saved. Hence, the line buffers gauss_xy_pixels and comp_edge_pixels can be reduced to two very small ring buffers of size 3x3. in_pixels is a ring buffer of size 3 after in-place mapping. The belonging source code fragment reduced to the ring buffer in_pixels looks as follows:
for (x=0; x
a += in_pixels[(x-1)%3] * 99;
a += in_pixels[x%3] * 68;
... }
The goal of Ring Buffer Replacement is to replace the data reuse copies by sets of local variables. Ring Buffer Replacement takes place in a two-step approach. First, a scalarization of ring buffers is performed. Second, loop unrolling guided by the characteristics of the ring buffers takes place. These two stages of Ring Buffer Replacement result in the following piece of code:
int ip0, ip1, ip2;
for (x=0; x
a += ip0 * 99;
a += ip2 * 68;
...
ip1 = img[...];
a = ip0 * 68;
a += ip2 * 99;
a += ip1 * 68;
...
ip0 = img[...];
a = ip2 * 68;
a += ip1 * 99;
a += ip0 * 68;
... }
The advantages of ring buffer replacement are manifold: