
Modern compilers provide a vast portfolio of optimizations which exhibit complex mutual interactions and affect different objective functions, such as WCET, ACET, code size, or energy dissipation in a hardly predictable fashion. Since compiler optimizations are not considered separately, the search for suitable optimization sequences and optimization parameters that promise a positive effect on a single or multiple objective functions is not straightforward. To cope with this problem, compiler developers construct standard optimization levels, like O3 or Os, which are based on their experiences. However, as previous studies have shown there is no guarantee that these optimization levels will also perform well on untested architectures or for unseen applications.
Concerning the code generation for embedded systems acting as hard real-time systems, the optimization problem becomes even more complex since these systems are characterized by both efficiency requirements and critical timing constraints. As a consequence, system designers of real-time systems must consider different objectives in a synergetic manner. Concerning the compiler-based code generation, there is no single compiler optimization sequence which satisfies all objectives. Therefore, multiple trade-offs must be considered enabling the system designer to choose among different solutions which best suit the system specifications.
The WCC compiler provides a modular and flexible framework to explore the performance of compiler optimizations with conflicting goals. Since typical state-of-the-art compilers provide a vast number of optimizations, the search space is too large to be exhaustively explored. To cope with this complexity problem, we apply evolutionary multi-objective algorithms which efficiently find a good approximation of Pareto fronts representing the best compromise between the considered objectives. The advantages of our framework are twofold. First, our techniques reduce the complexity of compiler design/usage by relieving compiler writers/users from the tedious task of searching for appropriate optimization sequences. Second, the automatically determined optimization sequences clearly outperform commonly used standard optimization levels, leading to higher system performance compared to traditional system design.
The structure of modern compilers is more or less rigid since optimizations are applied to an intermediate representation in a predefined order. This inflexibility is one of the major reasons why optimizing compilers do not deliver optimal performance. To address this problem, compilers must be extended in such a way that they can adapt to the compiled program and hardware. This adaptability is achieved by searching for promising optimization sequences that lead to a maximal improvement of the considered objectives. Compilers that provide this capability are known as adaptive compilers. The WCC also supports the application of optimizations in an arbitrary order, turning it into the first adaptive WCET-aware compiler.
This extension of a compiler significantly increases the search space of compiler optimization sequences, making an exhaustive testing infeasible. To cope with this huge search space, iterative compilation can be used. This technique is based on genetic algorithms where each optimization sequence is represented by a string where each character represents a particular optmiziation. Each generated optimization sequence is passed to WCC to generate code for which the objective functions are determined. Applying the operators crossover and mutation, the genetic algorithm tries to find better sequences for the next generation.
To cope with the multi-objective nature of embedded systems, a trade-off between different objectives has to be taken into account. As a consequence, optimizing the application w.r.t. a single objective might yield unacceptable results for other objectives, thus an ideal multi-objective solution, which simultaneously optimizes each objective, does not exist. To handle this problem, a set of solutions is determined. These solutions have the characteristics that on the one hand, each solution satisfies the objectives at a tolerable level and on the other hand, none of the solutions is dominated by another solution. Solutions meeting these characteristics are called Pareto optimal solutions. All these solutions can be visualized as a so-called Pareto optimal front. In practice, the number of Pareto optimal solutions is often too large. Therefore, the goal is to find a Pareto front approximation that minimally deviates from the Pareto optimal front. The relationship between a Pareto optimal front, its approximation, and dominated solutions for a minimization problem involving two objective functions is depicted below.
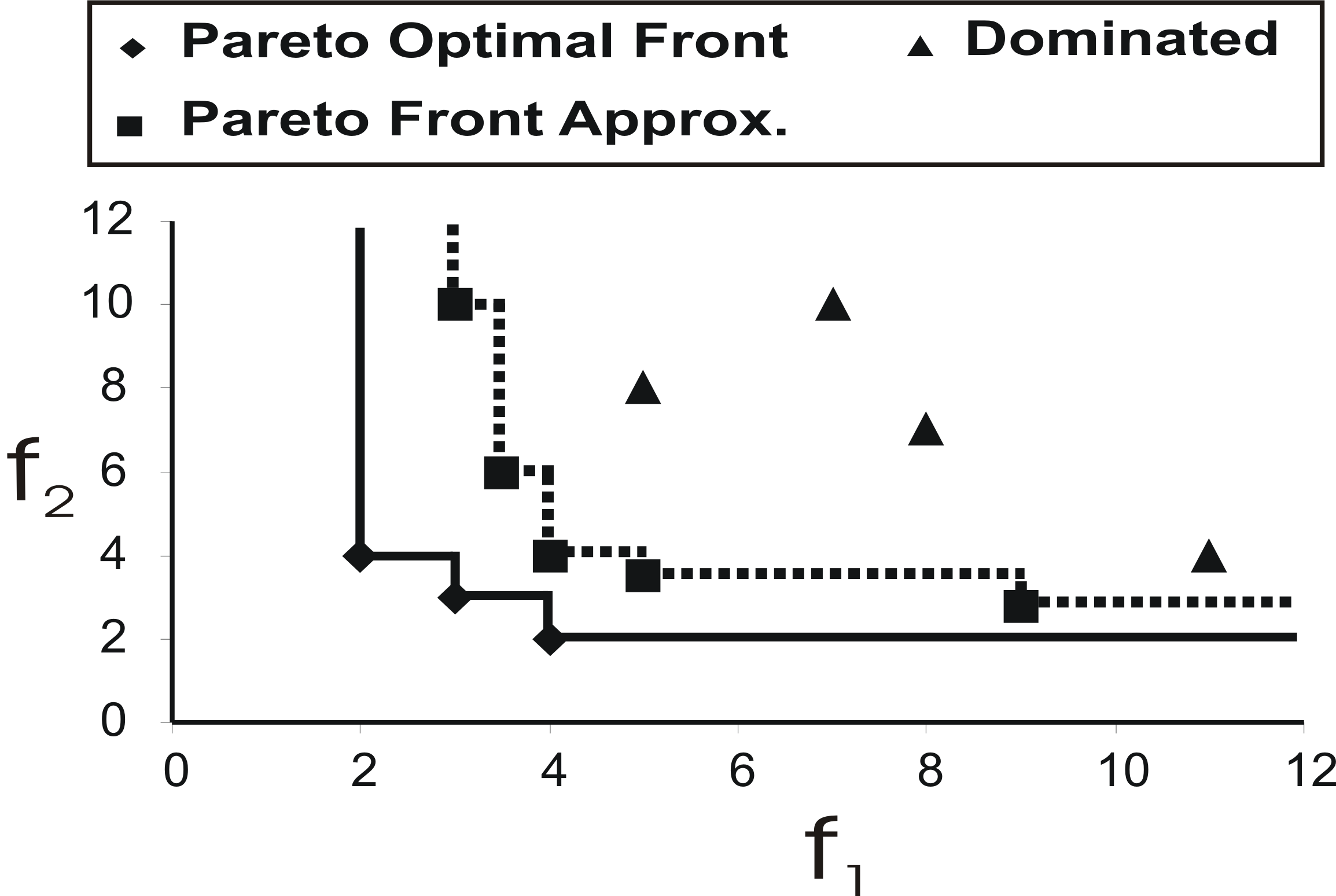
The Pareto front approximation can be finally used by to find suitable optimization levels. By constructing an approximation set for a large number of benchmarks, particular points from this set that satisfy given trade-offs between the considered objectives can be chosen. The optimization sequences that represent these points will be implemented as optimization levels into the compiler and can be used in the future for new applications.
To find Pareto front approximations, WCC uses evolutionary multi-objective algorithms. The goal of these algorithms is to find better front approximations for subsequent generations of solutions (optimization sequences). Since it is not straightforward to decide which evolutionary algorithm performs best for the exploration of compiler optimization sequences, WCC provides an automatic evaluation of different algorithms. This way, optimization sequences with the best performance can be found.
The multi-objective optimizations have been carried out for the objective pairs {WCET,ACET} and {WCET,code size}. The results are presented in the following.
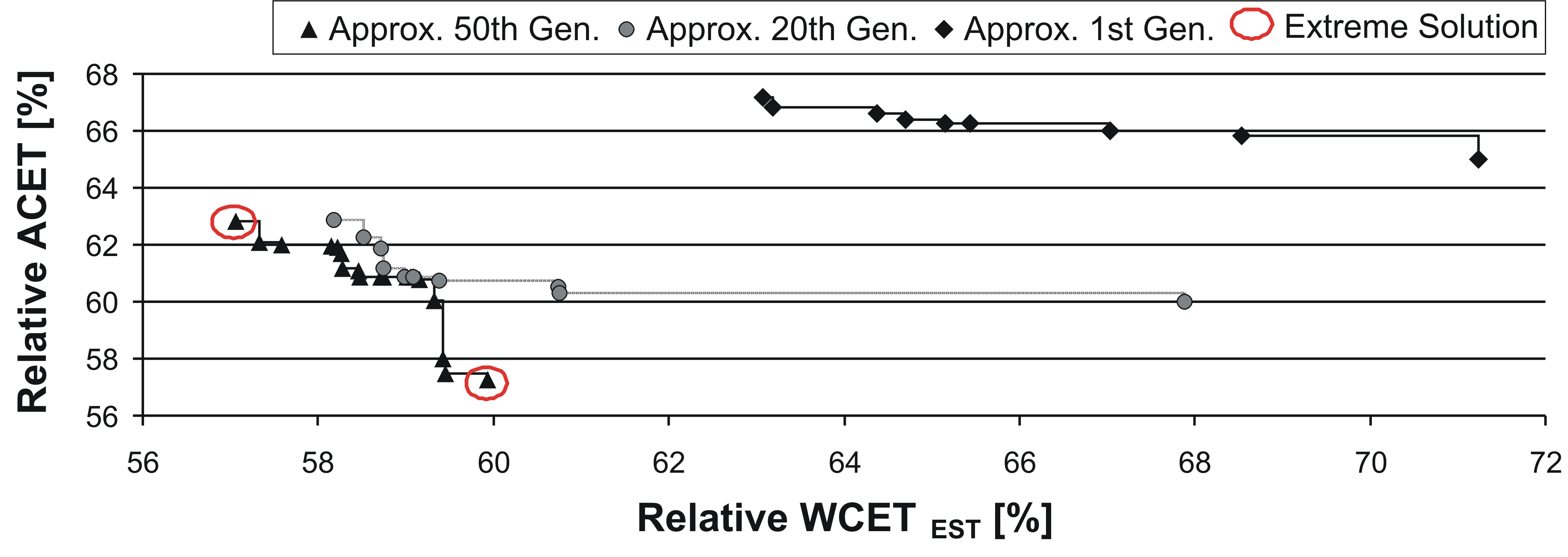
The above figure visualizes the Pareto front approximation generated by the algorithm NSGA-II which achieved best performance assessment results for the objective functions WCET and ACET. The horizontal axis indicates the relative WCET w.r.t. the non-optimized code, i.e., 100% represents the WCET with all disabled WCC optimizations. In a similar fashion, the vertical axis represents the relative ACET w.r.t. to the non-optimized code. Furthermore, the figure shows the results of the Pareto front approximation for the 1st, 20th, and 50th generation. Based on this figure, the following can be concluded:
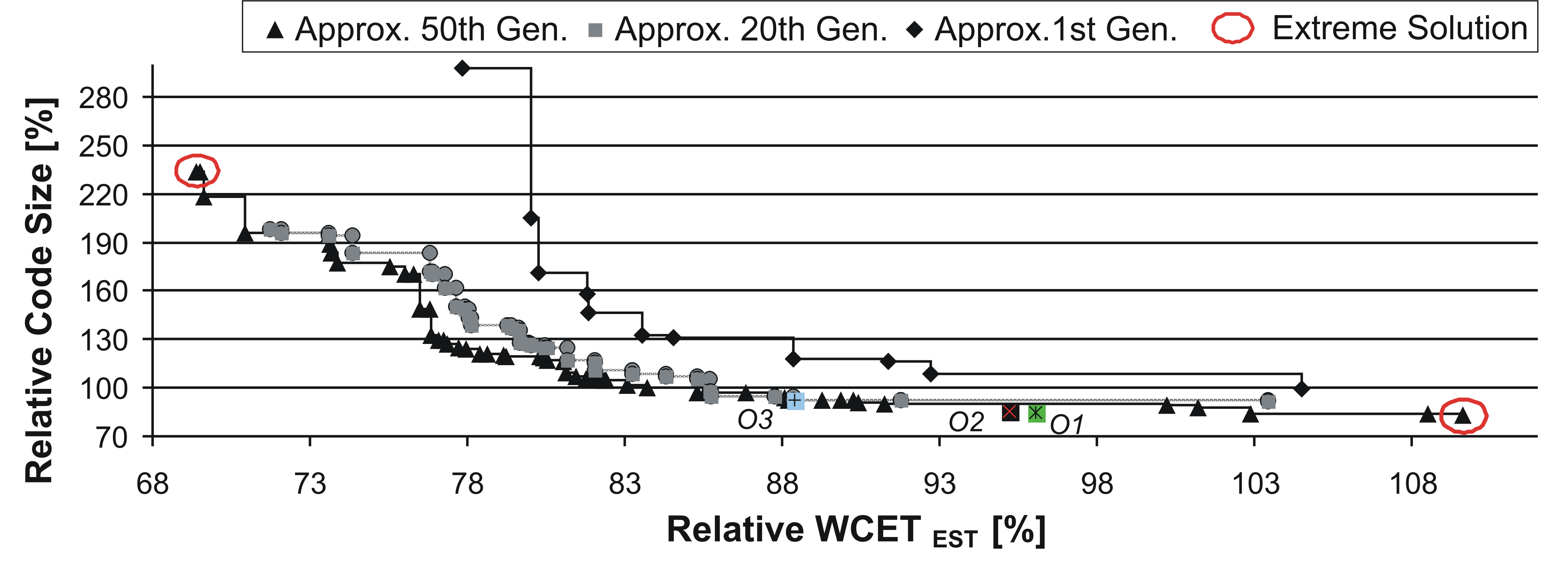
The Pareto front approximation computed by NSGA-II for the objectives WCET and code size is depicted in the second figure. The relative WCET w.r.t. the non-optimized code (corresponds to 100%) is represented by the horizontal axis, while the relative code size w.r.t. to the non-optimized code is shown on the vertical axis. Again, Pareto front approximations of the 1st, 20th, and 50th generation are visualized. Compared to the Pareto front approximations for {WCET,ACET}, the interpretation equals in two points:
However, there is also one major difference compared to the results of the objective pair {WCET,ACET}. The WCET and the code size are typical conflicting goals. If a high improvement of one objective function is desired, a significant degradation of the other objective must be accepted. This is an important conclusion for memory-restricted real-time systems. To achieve a high WCET reduction, the system must be possibly equipped with additional memory to cope with the resulting code expansion.