WCET Basics

Typically, an executable program exhibits a certain variability of execution times influenced by input data and interference from the environment. In the figure below, the distribution of possible execution times of some example program is depicted by the shaded area.

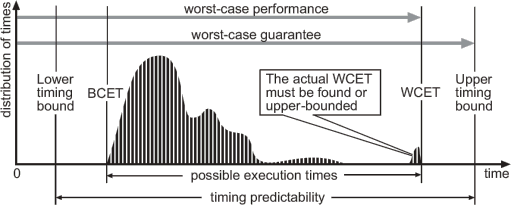
That point on the X-axis in the above program with the minimal execution time of the program is called the best-case execution time (BCET). Accordingly, the point representing the maximal execution time that a program can ever take is called the worst-case execution time (WCET). In between these two extremal points, the diagram shows all possible execution times of a program. That point in this diagram with the highest distribution is usually called the average-case execution time.

Unfortunately, it is in general very difficult or even impossible to determine the actual BCET and WCET of a program. Computing a program's WCET can be reduced to solving the halting problem which is known to be undecidable: If it were possible to compute the actual WCET of arbitrary programs, it is possible to determine in time complexity of O(1) whether this WCET is less than infinity, thus solving the halting problem. Instead of computing the actual BCET and WCET, reliable lower and upper bounds have to be determined by sound methods.

In the domain of hard real-time systems, WCET timing bounds have to fulfil the following two requirements:

• Safeness
  WCET timing bounds have to be safe which means that the bound must always be greater than or equal than the actual WCET. As shown in the above figure, safe WCET bounds thus have to be right of the actual WCET. An unsafe WCET bound is not reliable, because there would be actual execution times greater than the WCET bound which is unacceptable when designing hard real-time systems.
• Tightness
  The quality of a WCET timing bound can be expressed by the distance between the WCET bound and the actual WCET. The smaller this distance is, the better - or in other words: the tighter - is the WCET bound.