
Even though source-level flow fact specification and automatic flow fact transformation is already very convenient, it is desirable to take the burden of manual flow fact specification completely away from the user. For this reason, WCC is equipped with a highly sophisticated loop analyzer generating flow facts within the ICD-C compiler framework in a fully automated fashion.
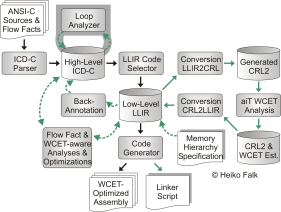
WCC's loop analyzer bases on the techniques of Abstract Interpretation, Interprocedural Program Slicing and Polyhedral Loop Evaluation. WCC's loop analyzer has proven to be of superior quality - among all tools participating in the WCET Tool Challenge 2008, it was the only one which was able to solve all flow facts related analysis problems.
Abstract interpretation is a theory of sound approximation of mathematical structures. It is mainly used to approximate semantic models of computer systems. Its main field of application is static program analysis which exploits the fact that undecidable or very complex problems can be solved if incomplete results are tolerated.
Static loop bound analysis is an example for an undecidable problem. For concrete program semantics, the automatic determination of loop iteration counts for arbitrary loops is not feasible. By introducing abstract semantics, which is a superset of the concrete semantics of a program that covers all possible actual cases, the loss of information turns the analysis computable.
The fundamental idea behind abstract interpretation is to find an appropriate compromise between the precision of the analysis and its run time. This reduction of information is achieved by mapping a potentially infinite set of program states - typically consisting of the value of the program counter (program point) and a set of variables (or memory locations) - to a finite set of abstract states. The objective of a static analysis based on abstract interpretation is to assign sets of possible variable values (abstract states) to edges of a control flow graph.
However, abstract interpretation suffers from its typical iterative behavior slowing down the analysis such that it may become infeasible when being applied to realistic programs. In particular, such an explosion of analysis times can be observed during the analysis of loops with high iteration counts where each loop iteration is interpreted individually.
WCC's innovative loop bound analyzer combines abstract interpretation with mechanisms avoiding its iterative behavior. These mechanisms rely on interprocedural program slicing and polyhedral loop analysis determining loop iteration counts and variable values by iterating the loop body exactly once. If these advanced techniques succeed in computing loop bounds, classical abstract interpretation is omitted for this loop. Otherwise, classical abstract interpretation needs to be applied.
Program slicing is an analysis technique finding statements of a program that are relevant for a particular computation. It defines how a given program can be sliced w.r.t. a slicing criterion. A slicing criterion is defined to be a pair where q is a program point and V is a subset of program variables at q. The slice for a given program w.r.t. defines a subset of the program containing all statements which might affect the variables in V.
Within the WCC compiler, interprocedural program slicing is applied w.r.t. loop exit conditions. By taking all relevant data and control dependencies into account, the resulting program slice contains all statements that are involved in the determination of loop iteration counts. WCC's slicing is accompanied by a context-sensitive alias analysis to support pointers. Contexts introduce a distinction between different calls to a particular function, thus allowing for a more precise analysis.
In the WCC setup, program slicing is run before the actual abstract interpretation-based loop analysis for two reasons:
A polyhedron is an N-dimensional geometrical object defined by a set of linear inequations:
P := { x ∈ ZN | Ax = a, Bx ≥ b }
for A,B ∈ Ζm×N and a, b ∈ Ζm and m ∈ Ν. A polyhedron is called a polytope if
|P| < ∞
Polytopes are often employed in compiler optimizations since they can be exploited to represent loop nests and affine condition expressions.
Polyhedral loop evaluation within WCC is motivated by the observation that a large number of loops consists of statements not affecting the calculation of loop iterations. Typical examples are initialization procedures found in many embedded applications. The main task of such procedures is the initialization of arrays and other data structures. Afterwards, this initialized data is involved in the computation of output data, e.g. an output stream of an image compression algorithm, but it is not influencing the execution frequency of loops. Using program slicing, those statements are recognized to be meaningless for loop analysis and are excluded for further evaluation. This frequently results in loops with almost empty loop bodies.
Polyhedral evaluation is applied to loops fulfilling the following prerequisites on the loops' structure and the type of statements within the loop body:
It should be noted that these prerequisites are often met by well-structured loops found in many applications. Thus, they do not inhibit the successful application of polyhedral loop evaluation to realistic programs in practice.
If all preconditions are met, loop iteration counts are statically determined by computing the number of integer points in the polytopes representing the actual loop. To efficiently count all integer points, Ehrhart polynomials are used.
However, taking all integer points of a polytope into account might yield an over-approximation for many loops. The total number of integer points represents the number of loop iterations if the loop counter is incremented by one. For other modifications of the loop's induction variable, the number of counted points has to be adjusted appropriately. Also, additional exit edges that affect the control flow in the loop body, e.g. in the case of break or continue statements, should be taken into account. They are modeled as further polytopes, and their intersection with the polytope representing the whole loop nest yields the precise solution space to which Ehrhart polynomials are finally applied.
Based on the knowledge of loop iteration counts, the execution frequencies of conditionally executed basic blocks, which might obviously differ from the loop iteration counts, are determined. The conditions guarding such basic blocks are again represented as polytopes, and their intersection with the loop polytope allows the calculation of execution frequencies for both their then- and else-parts.
The last step during polyhedral loop evaluation deals with the static evaluation of statements within the loop body, based on the loop iteration counts and basic block execution frequencies computed in the previous stages. Here, the goal is to evaluate modifications of variables within the loop like e.g. b += a; without applying repetitive abstract interpretation. The variable values determined this way are used to compute iteration counts for loops that are analyzed afterwards using classical abstract interpretation.