
Many architectures are equipped with fully software-controllable secondary memories. These are memories that are tightly integrated with the CPU to achieve best possible performance. These scratchpad memories (SPMs) can be accessed directly and are therefore in general well-suited for optimizations regarding energy consumption and execution times.
For WCET-centric optimizations, a scratchpad memory is ideal since the timing of such memories is fully predictable. Within the WCC compiler, SPMs are exploited for WCET minimization by placing assorted parts of a program into a scratchpad memory. This page describes strategies based on integer linear programming (ILP) for moving parts of a program's code and data onto SPMs.
Since the TriCore processor architecture supported by the WCC compiler features independent scratchpads for code and data, the corresponding ILP formulations for both types of scratchpad memories are very briefly sketched independently in the following.
In order to move individual basic blocks of a program onto a scratchpad memory, the generated ILP uses a binary decision variable xi per basic block bi. bi is moved onto the scratchpad memory if xi is equal to 1. The overall goal of this ILP is to find an assignment of values to the variables xi such that the resulting scratchpad allocation leads to a global WCET minimization.
A legal scratchpad assignment needs to make sure that the size of all basic blocks assigned to the scratchpad memory does not exceed the scratchpad's capacity. This is ensured by the following capacity constraint:
x1 * size1 + x2 * size2 + ... ≤ SPM_Size
In addition to this capacity constraint, other constraints need to be added modeling the structure of a program's control flow graph (CFG). The generation of these constraints starts with all those basic blocks bi located in the innermost loops including no other loops inside them. For each such block bi and each successor bi+1 of bi in the CFG, a constraint is set up bounding the WCET Wi of bi:
Wi ≥ Wi+1 + costi,main_mem - gaini * xi
This constraint states that the WCET of bi has to be larger than that of any of the successors of bi, plus the contribution of bi to the WCET itself with bi located in main memory, minus the potential gain when moving bifrom main memory onto the scratchpad memory. This way, constraints for all blocks of the innermost loops can be set up.
The WCET of the body of such an innermost loop is thus represented by the variable Wfirst_node(loop) for the very first basic block of the loop body. Since a loop executes its body several times, the entire loop's WCET is constrained by:
Wloop = Wfirst_node(loop) * iteration_count(loop)
where the iteration count of a loop is taken from its annotated flow facts within the WCC compiler. Whenever an outer loop L1 contains another loop L2, this inner loop L2 is treated as a single CFG node with a WCET represented by the ILP variable WL2 as defined above.
Analogously, the WCET of a program's function is represented within the ILP by the variable Wfirst_node(function) for the very first basic block of this function. If function calls are modeled correctly within the ILP, an entire program's WCET is finally represented by the variable Wstart_node(program) of the program's entry point. Since a program's WCET is to be minimized by this integer linear program, its objective function is as simple as shown below:
Wstart_node(program): minimize
In addition to the above constraints, the ILP formulation produced by the WCC compiler also takes care of adjusted branch instructions making sure that a basic block located in main memory can branch to a successor placed onto the SPM, and vice versa.
The structure of the ILP formulation responsible for allocating program data to a scratchpad memory is very similar to the ILP described above for SPM allocation of code. In order to allocate data to a scratchpad memory, binary decision variables yj are introduced per global variable vj (or per local variable declared to be static). The meaning of these variables vj is analog to the variables xi introduced previously.
The most important difference between both ILPs lies in the definition of the gain gaini per basic block bi. In the case of program data, a gain is achieved for basic block bi if some of the variables vj accessed by bi are moved from main memory to the SPM. The data access behavior of a basic block bi required to formulate gaini is determined by a context-sensitive static alias analysis and by the static WCET analyzer aiT.
There are other minor differences between the ILP formulations for code and data SPM allocation, but for the sake of clarity, they are not described here.
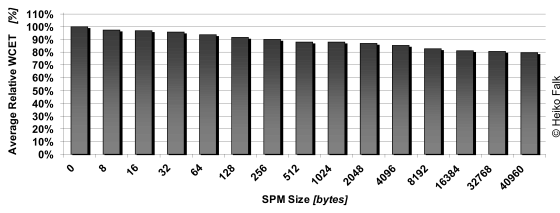
The above figure depicts the effect of scratchpad memory allocation of data on the resulting WCETs. It shows the average WCETs over a set of 14 different benchmarks for various different scratchpad memory sizes. The 100% base line thus reflects the WCETs of the benchmarks without using the data scratchpad memory at all. This diagram assumes the TriCore TC1796's memory hierarchy where an access to the DMU SRAM (i.e. the slower main memory) takes 6 cycles and an access to the DMI-LDRAM (i.e. fast scratchpad memory) takes 1 cycle.
As can be seen from this diagram, considerable WCET reductions are achieved already for very small scratchpad memories with only a two-digit size: for example, using a 64 bytes small SPM leads to average savings of 6.5%. With increasing SPM sizes, the achieved gains also increase as shown in the figure, since the WCC compiler is able to move more and more data onto the larger SPMs. For a total SPM size of 40kB which corresponds to the real scratchpad size of the Infineon TC1796 processor, total average savings of 20.2% were achieved by the SPM allocation of data described here.
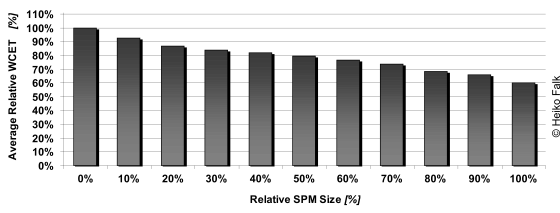
Last but not least, the above figure shows the impact of SPM allocation of program code on the resulting WCETs. It shows the average WCETs over a set of 73 different benchmarks for various different scratchpad memory sizes. Again, the memory hierarchy of the Infineon TriCore TC1796 is assumed here, resulting in a latency of 20 cycles per access to the PMU-PFLASH and 1 cycle per access to the PMI-SPRAM.
In contrast to the previous figure, SPM sizes are not shown in absolute byte-values. Instead, SPM sizes relative to the total code size of the benchmarks are used. Hence, the category '20%' shows the WCETs for a scratchpad size of 20% of the entire code size. Once again, the 100% base line reflects the WCETs of all benchmarks without using the program scratchpad memory at all.
It can be observed that the improvements due to program scratchpad memory allocation are even larger than those encountered when moving data onto SPMs. This is not surprising since instruction fetches occur more often than load or store operations to data memory. In analogy to the results for data SPM allocation, already very small program SPMs with a size of only 10% of the total code size lead to considerable average WCET reductions of 7.4%. As already observed above, the savings in terms of WCET increase with increasing SPM sizes. For SPMs large enough to hold the entire program, WCET reductions of 40% were observed on average over all considered benchmarks.